
大切な情報を流出させないように、「暗号」というものが現在でも使用されています。
暗号は古代から使用されており、暗号の歴史は暗号開発者と解読者との繰り返しで、どんどん強化していきました。
小学生向けの暗号問題から、歴史上の暗号、現在の暗号を簡単にして紹介しています。
目次
頭の体操問題

まずは、頭の体操の問題を3問ほど。
第1問
□に入る文字はなにか。
親 人 中 □ 小
第2問
□に入る文字はなにか。
北 本 □ 九
第3問
□に入る文字はなにか。
S M T □ T F S
頭が柔らかくなってきたところで、暗号を解読に挑戦してみてください。
小学生向けの暗号

小学生向けの暗号クイズです。難問も入っています。
第4問
??にあてはまる数字はなにか。
7=2 8=2 3=3 5=4
9=??
第5問
??にあてはまる数字はなにか。
6668=5
5901=2
0060=4
1985=??
第6問
難問です。??にあてはまる数字はなにか。
22△5=90
11△3=27
52△4=192
35△1=??
歴史上の暗号
第7問 シーザー暗号

ローマ軍の指揮官ユリウス・カエサルの使者から
\( XNQT , JNTFDJH \)
と書かれた紙を受け取った。どうすればいいのか??
①籠城する(城にこもる)
②増援を送る
③夜間奇襲する(夜に攻撃する)
解説

A→Bというように1文字だけアルファベットを右にシフトすれば、
\( XNQT , JNTFDJH \)
X→Y,N→O, Q→R , T →U・・・・となり、
\(YORU , KOUGEKI\)
「よる、こうげき」となります。
ここでは、右に1文字ですがカエサルはn文字ずらして、敵に重要な情報を見破られるのを防いでいたみたいです。
因みにユリウス・カエサル(英語読みジュリウス・シーザー)からシーザー暗号と言われています。
数世紀に渡って使用されましたが、25通り調べれば解読することができるため、徐々に複雑になっていきました。
第8問 上杉暗号
日本では暗号文化は薄く、有名なのが軍神と恐れられた越後の竜「上杉謙信」。

問題
あることで武田軍が苦しんでいる。そこへ上杉謙信公の使者から、
「32 15 105 15 23 94」
と書かれた手紙が渡された。
武田軍に対してどうすればいいのか?
①すぐに攻撃する
②もっと苦しめる
③物資を送る
解説

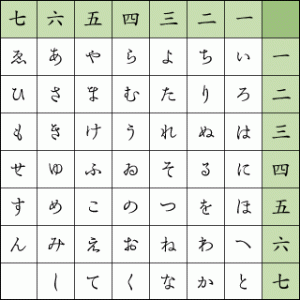
「32 15 105 15 23 94」
| ・・ | 3 | 2 | 1 | |
| ・・ | さ | か | あ | 1 |
| ・・ | し | き | い | 2 |
| ・・ | す | く | う | 3 |
| ・・ | せ | け | え | 4 |
| ・・ | そ | こ | お | 5 |
32→し、15→お、105→を
15→お、23→く、94→れ
「しおをおくれ」となります。義の男、上杉謙信らしい行動と感じます!
上杉謙信の軍師、宇佐美定行がこのような暗号を考案したと云われています。
実際には、いろはにほへと・・・と続く平仮名を7×7に置き、平仮名に対応する数字を暗号化したものです。換字式暗号の一種。
この暗号のおかげで、セキュリティ面が大幅に強化され軍事情報や政治情報などの機密が他国へ漏洩されることがなくなりました。
95%以上の勝率を誇る上杉軍を影で支えていたのは間違いありません。
ちなみに、25年くらい前にポケベルっていうものが流行りましたが、ポケベルもこのような換字式暗号です。
現代の暗号

第9問 RSA暗号
RSA暗号はアメリカのリベスト、シャミア、アドルマンによって開発され、それぞれの頭文字をとって名付けられました。
問題
2279 を素因数分解せよ。
解説
この程度の数字でも、素因数分解するのは大変です。しかし、
現代の暗号を突破するには、300桁以上の数字の素因数分解が必要になってきます!!
\(43 × 53 = \)
の計算は容易にできますが、
\(2279 = x × y \)
xとyを求めるのは困難になる、という発想から開発されています。
仕組みは合同式の性質・逆元・フェルマーの小定理・オイラー関数の性質などを使っています。
(高校以上の知識が必要になります)
どんな所で使われているのか?

無線LAN・https・電子申請書の本人確認・クレジット決済など。
インターネットには多く使用されています。
安全性は??

先ほど言ったように、RSA暗号を突破するには300桁以上の数字の素因数分解が必要になります。
現代のパソコンが計算しても、もの凄い年月がかかると言われています。
RSA暗号は解読不可能を目指したのではなく、解読できるが簡単にはできない。。というシステムです。
もし解読できたとしても、その時には何の役にも立たない情報となっている、ということです。
暗号 まとめ
古くから軍事・政治の場面での利用から発達した「暗号」。
歴史からわかるように、暗号を開発すれば、解読するものが現れます。
解読すれば、また新しい暗号がうまれ、そして、また解読。。
その背景には数学があり、暗号の発展とともに科学も発展しています。
現在は量子コンピューターという研究をしており、これが完成すればRSA暗号は一瞬にして解読されてしまうみたい。(まだまだ20年以上先のことみたい)
しかし、そのコンピューターが出来るころには、「量子暗号」ができる。
暗号の戦いは、終わりなき戦いです!
























