
死刑囚(個人戦)
問題
以前に釈放された3人の死刑囚A,B,Cはまた犯罪を犯した。そして、死刑執行の日がやってきた。そこで王様は、

王様
これからあるゲームを行い、それに勝てば釈放してやろう!
と言った。
ゲームのルール
- 赤と白の帽子が2つずつある
- 赤か白の帽子を3人に被せる
- 自分の帽子の色はわからない
- 自分の帽子の色を当てる
上記が基本ルールである。そして、
- 3人は横1列に並び、前・真ん中・後ろをくじ引きで決める
- 前にいる人の帽子の色は見える、帽子の色を当てる声も聞こえる
- 正解すれば釈放・間違えれば死刑執行
- お互いに何かの合図を送ったりした場合は死刑執行
といった内容を説明した。そして、
- 死刑囚Aが前
- 死刑囚Bが真ん中
- 死刑囚Cが後ろ
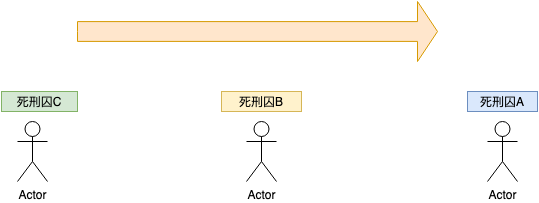
となった。
ゲームが始まりしばらくすると、一人が釈放された。
一体誰が釈放されたのか??
ヒント
すぐにではなく、、しばらくすると。
解答
死刑囚Bである。
解説
①死刑囚Aの場合
死刑囚Aは先頭で何も見えないので、答えることができない。
②死刑囚Cの場合
死刑囚Cは、AとBが(赤・赤)(白・白)の場合は、すぐに答えることができる。
しかし、(赤・白)(白・赤)の場合は、答えることができない。
問題文では、しばらくすると・・と書いてある。つまり、(赤・白)(白・赤)だったということ。
③死刑囚Bの場合
死刑囚Bは、後ろのCがすぐに答えないということは、、
(赤・白)(白・赤)ということに、しばらくすると気づく。
先頭のAの帽子の色を見ることができるので、Aと違う色を答えればいいことになる。
補足

この問題の場合は、この後先頭のAも釈放される。Bが答えた色と違う色を言えば正解となるからである。
更にもう1つ説明!!すべての帽子の組み合わせは、
組み合わせ
①(赤・赤・白) ②(赤・白・赤) ③(赤・白・白)
④(白・赤・白) ⑤(白・赤・赤) ⑥(白・白・赤)
の6通りです。
- 死刑囚Aは、①・②・④・⑥の4通りで釈放される。
- 死刑囚Bはすべての場合で釈放される。
- 死刑囚Cは③・⑥の2通りで釈放される。
※一番有利に思える死刑囚Cが実は一番不利になっていることがわかる。





















