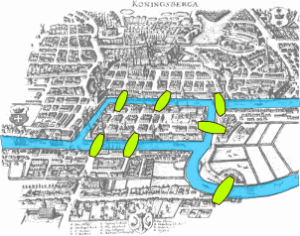
一筆書きとは・・鉛筆などを一度も紙から離さず図形を描くことです。

この図形は一筆書きで描けます。
ではこれはどうでしょうか??
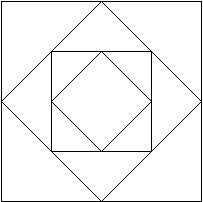
(※最後に解答あります!)
これは数学パズルの定番の問題で、一筆書き問題というものです。
実はこの一筆書きにはある法則が隠されていました!
そして、この単純なパズルから数学のある分野が発展していきます。
この法則に気付いた最初の人物とは誰なのか??
ケーニヒスベルクの七つの橋
問題
18世紀初期、プロイセン王国の東部に東プロイセンという国があった。
その国の首都にはケーニヒスベルクという大きな町があり、
この町の中央にはプレーゲル川という大きな川が流れており、七つの橋が架けられていた。
あるとき、町の人が

と言った。こんなことができるのだろうか??
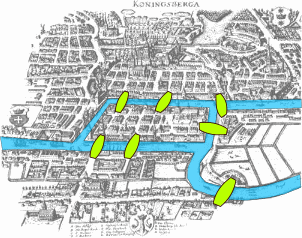
wikipediaBogdan Giuşcă 氏によるThe problem of the Seven Bridges of Königsberg.CC 表示-継承 3.0
ブレーゲル川と7つの橋を示したケーニヒスベルク
解答
できない。
解説

これを証明したのは、レオンハルト・オイラーです。
オイラーはこの問題を

と考えました。つまり、

- wikipedia CC 表示-継承 3.0
fa-arrow-circle-down
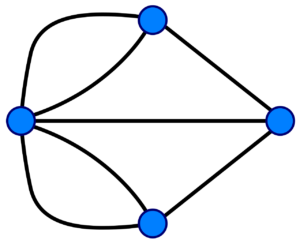
- wikipedia Königsberg graph CC 表示-継承 3.0
このようにこの町をグラフ化して考えました。
このグラフが一筆書きできれば問題が解決するからです。
そして、一筆書きができる条件を2通りに分けて考え、あることに気付きます。
- スタートとゴールが同じ(閉じた場合)
- スタートとゴールが違う(開いた場合)
スタートとゴールが同じ場合

この図形では、A~Dどこからスタートしてもゴールが同じ場所になります。
そして、どの頂点も集まってきている線が2本(偶数本)であることに気付くと思います。
スタートとゴールが同じ場合には、
どの頂点も集まってくる線(次数)が偶数ってことです。
スタートとゴールが違う場合

上の図はDかEからスタートしなければ、一筆書きができません。
そして、D→EかE→Dでゴールするようになってます。
Dの次数は3、Eの次数は1、残りは2です。
つまり、次数が奇数の頂点が2個で、残りの頂点の次数は偶数です。
スタートとゴールが違う場合には、
次数が奇数の頂点が2個だけで、残りの頂点の次数は偶数。
一筆書き判定
これらをまとめると、一筆書きができるかどうかの判定は
- 頂点の次数が全て偶数
- 2つの頂点のみ次数が奇数、残りは偶数
この2つの場合だけ可能とわかります。
実際に確認してみてください。
①頂点の次数が全て偶数の図形

2つの図形は、どの点からスタートしても一筆書き可能です。
②2つの頂点のみ次数が奇数、残りは偶数

この図形は、AかBの点からスタートすれば一筆書き可能です。
ケーニヒスベルクの七つの橋

- wikipedia Königsberg graph CC 表示-継承 3.0
一筆書きができるかどうかの判定は
- 頂点の次数が全て偶数
- 2つの頂点のみ次数が奇数、残りは偶数
だけです。
このグラフは、頂点の次数が3,3,3,5とすべて奇数となってます。
①と②に該当しないため、一筆書きを描けない。
つまり、この問題は元に戻ってくることはできない!!ってことになります。
この問題からグラフ理論が発展していきました!
最初の問題
この図形は一筆書きできる図形か??

解答
できます。
解説

まず頂点の次数を調べます。
頂点の次数が全て偶数とわかります。
一筆書きの判定は
- 頂点の次数が全て偶数
- 2つの頂点のみ次数が奇数、残りは偶数
であるので、
①に該当するので、この図形は一筆書きできます。
どの頂点から始めても、その場所に戻ってくることができる手順がありますので、根気よく確かめてみてください!!