
「お母さん、100円ちょーだい。」
「明日7時に起こして。」
など、日常生活で当たり前のように数字を使っていると思います。
数字は古代から使用されていて、数字はものを数える中で生み出された人類の知恵です。
そして、長い年月をかけて今の数字の考え方までたどり着いています。
ここでは、数の歴史について紹介していきます。
実数
自然数


この図を見比べて、共通点を考えるときに
人間の頭の中に浮かぶのが「2」という考え方でした。
そして、この考え方が「自然数」という概念となりました。
自然数とは 1,2,3・・・ のような 正の整数
\(5+7=12\)
自然数に自然数を足せば、必ず自然数になります。
\(5×7=35\)
自然数に自然数をかけても、必ず自然数になります。
これで大きい「個数」でも、簡単に計算できるようになりました。

分数
しかし、5mを7等分した長さなど
\(5÷7=??\)
自然数に自然数で割れば、自然数にならない数字が出てきました。
そこで5mを7等分した長さを\({\frac{5}{7}}\)のように表し
これらを分数と決めました。
有理数
自然数と分数を合わせて有理数になりました。
(現在の有理数とはまだ解釈が違います!!)
自然数では「個数」の計算しかできませんでしたが、
有理数では、長さ・重さ・面積など「量」を数で表すことが可能となりました。
ピタゴラスの非情

三平方の定理で有名なピタゴラスは、
「有理数が数のすべてであり、有理数であらわせないものはない!!」
とピタゴラス教団で弟子達に説いていました。
ところが、弟子のヒッパソスが、
「・・・有理数では決してあらわせない量がある」
ということを発見してしまいました。
これに激怒したピタゴラスはヒッパソスを溺死させてしまいます。
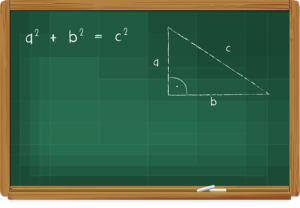
三平方の定理
\(\Large{x^2 + y^2 = z^2}\)
無理数
ヒッポソスが発見した「有理数ではあらわせない量」は正方形の対角線に潜んでいました。
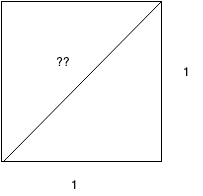
1辺の長さが1の正方形の対角線の長さは、三平方の定理より
\(x^2 + y^2 = z^2\)から
\(\Large{1^2 + 1^2 = 2}\)となります。
つまり、\(\Large{ z^2 = 2}\)です。
これは、対角線の長さは2乗して2になる数 ということです。すなわち2の平方根。
こんな有理数を見つけることは決してできません。
自然数の分数であらわすことのできない数を無理数と決めました。
\(\Large{\sqrt{2}=1.41421356・・・}\)
\(\Large{\pi=3.14・・・・}\)
0という考え

私たちは、普通に「0」を数字として扱っていますが、実は長い間0は数字としてみなされませんでした。
そして、0という考えは様々な人を悩ませていました。
\(\Large{0-4=?}\)
この答えはー4です。
正の数・負の数を習っていればすぐにわかると思います。
しかし「人間は考える葦である」で有名な数学者パスカルの答えは、

と考えました。ゼロは何もない無だから、何も引けないという考えです。
\(\Large{4÷0=??}\)
0の割り算はもっと大変です。どう考えればいいのか??
\(4÷0=a\)とします。
すると、\(4=a×0\)となり、
aがどのような値をとっても、\(\Large{4=0!?}\)となります。
このように0は、取り扱い方によって数学を崩壊させる力を持っていました。
ヨーロッパでは敬遠されていて、ゼロを数としてみなしたのはインドが最初といわれています。
負の数という考え

「-30℃の世界」
「-15点」
など現在は生活の中にも、負の数が使われています。しかし、負の数も0と同じでした。
ヨーロッパでは2次方程式の解などで、負の数があることを知っていました。
しかし、実生活では何の役にも立たないので、意味のない数として扱われていました。
インドの銀行

負の数を実生活でも利用していたのが、0と同じインドでした。特に銀行で利用されていました。
銀行では、毎日たくさんの人がお金を預けたり・お金を借りたりしています。
マイナスという考えがなければ、計算が大変なんです。
さて、今いくらお金を借りていますか??
・・・この問題少しややこしくないですか!?
これを
\(貯金 → +円\)とし \(借金 → -円\)のようにマイナスを使えば
となり、62,000円の借金となります。
このほうが計算も楽になり、管理するのも簡単になります。
※ヨーロッパで0や負の数が認められたのは16世紀ぐらいと言われています。
(因みにフィボナッチ数列で有名なフィボナッチが、ヨーロッパで0や負の数という考えを広めたように言われています。)

これで、自然数・分数・0・負の数という考えが一般的に理解されました。
そしてこれらが、現在の有理数となっています。
有理数と無理数を合わせて実数となりました。
次回、虚数。






















