天下分け目の関ケ原で勝利した徳川家康。
1603年に江戸に幕府を開いた時代に、果たして数学があったのか??
またどの程度のレベルだったのか??
江戸時代に数学はあったのか??
塵劫記

江戸時代初期の1627年に吉田光由が執筆した算術書
「塵劫記」(じんこうき)
が発売されました。
この塵劫記が全国的に爆発的な大ヒット!!
老若男女問わず農村部から都市部まで空前の数学ブーム!!
江戸時代初期にはなんと、日本全土が数学に熱中していたんです。
塵劫記の内容
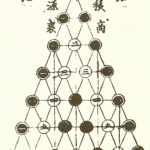
塵劫記の内容は
- 九九・そろばんのマニュアル
- ねずみ算・カラス算
- 俵杉算・油分け算
- 方陣
など小学校卒業までの知識で解ける問題をイラスト付きで出版していました。
塵劫記が大ヒットした4つの理由
- 戦国時代を抜けて人々の生活に少し余裕がでてきていたこと
- 難しい内容ではなく、子どもでも理解できること
- 実生活に関係のある多くの問題があったこと
- イラストが付いていたこと
以上の理由から長期に渡ってのベストセラーとなりました!
そして、数学の入門書で数学の面白さを知った人たちが各地で塾を開いていきました。
そこでは身分制度を越えて繁盛し、子どもも女性も数学を楽しんでいたと言われています。

塵劫記の海賊版 から 新塵劫記 へ

しかし、良い面ばかりではありませんでした。
有名となった塵劫記ですが、全国で次々に粗悪な海賊版「塵劫記」が出版されていきました。
そのことに嘆いた吉田光由は、
「・・・節単に云わんとする所を書けば、世の中にはさほど数学の力もないのに塾を作り、多数の人を教えている人がいる。自分の師が力があるかどうかわからないだろう。そろばんの計算が速いからといって数学の力があるとは決まっていない。ここに法(答えまでの道筋)のない十二問の問題を出しておくから、これで自分の師を試してみればよい。」
と 「新塵劫記」 を出版しました。
これは、答え・解法を記さない遺題として世に広まっていきました。
力のない数学者は、

と焦ったと思います(笑)
新塵劫記の内容
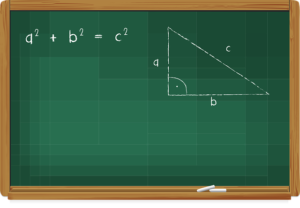
- 連立方程式
- 二次方程式
- 三平方の定理
- 難問 三次・四次方程式
※桧木5 本,松の木3 本,杉の木4 本を三色合わせた値段が銀で275 目、
※桧木3 本,松の木6 本,杉の木6 本を三色合わせた値段が銀で300 目、
のときおのおのの木は1 本いくら か。
(解説) 桧・松の木・杉の木の単価をそれぞれx, y, z 目とすると
2x+4y+5z=220・・・・・・・・・(1)
5x+3y+4z=275・・・・・・・・・(2)
3x+6y+6z=300・・・・・・・・・(3)
x=30 , y=15, z=20 答え 桧30 目, 松の木15 目, 杉の木20 目
など中学数学以上のレベルが必要であり、難問では4次方程式までありました。
遺題継承

新塵劫記の内容は当時の人達には難しい内容でしたが
さすが数学大国日本!!
力のある数学者が解いては遺題を残すという、遺題スパイラル!
これは遺題継承と呼ばれ発展してきました。
難しい問題を解いては、さらにその上のレベルの問題を出し、さらにその上、さらに・・・・・
と数学界が大いに盛り上がり、そして新たな技法が必要となってきます。
古今算法記
沢口一之は「古今算法記」で当時難問であった遺題を解き、
中国の算術書「算学啓蒙」に載っている技法、天元術の威力を世にしらしめました。
そして、沢口もスパイラルにのっかかり天元術だけでは解けない遺題を15題記します。
天元術では4次方程式でも解くことができましたが、2つの文字がある方程式では無理でした。
しかし、遺題には多元方程式が記されていて、当時の人達には全く歯が立ちませんでした。

関孝和
発微算法

ここで関孝和が登場します!!
「発微算法」という著書で沢口の遺題をすべて解きます。
この時に天元術を更に発展させた傍書法(後に点ざん術)を披露します。
優秀な弟子達

関孝和以前の数学者は、個々の問題を解くことを主眼にしていました。
一方、関は一般論の構築を重要と考えていました。
なので当時の人たちには理解されず、批判するものも少なくありませんでした。
しかし関には優れた弟子達がたくさんいました。
関のことを評価しない世間に対し、弟子達は不満爆発!
弟子の建部が「発微算法解説」を発表します。
発微算法解説
大学受験をする人なら覚えておきたい重要公式
\(x^3+y^3+z^3-3xyz の因数分解\)
などを使用して、関が沢口の遺題を解いたことを詳細に解説しました。
と人々は関を評価し始めました。
括要算法

その後、弟子たちが「括要算法」を発表。そこには
- ベルヌーイとは違う独自のベルヌーイ数
- 連立一次合同式
- 正多角形の内接円・外接円の半径を求める方程式
が書かれていました。特に有名なのは円周率。
正\(2^{17}\)角形 (131,1072角形)!!!
アルキメデスが正96角形を求めて、
\(3+\frac{10}{71}<\pi<3+\frac{1}{7}\)
という関係を導きましたが、関は小数第11位まで計算しています。
東大入試問題

少し話しが変わりますが、円周率が出てきたので余談をちょっと・・。
「ゆとり教育で円周率が3になるかもしれない。」
ということが社会全体に広く認識されるようになっていました。(一部マスコミの誤解みたい。)
そこで、東京大学の入試問題で
Q.円周率は3.05より大きいことを示せ。
という問題が出されました。
恐らく東大の教授たちはこのように考えたんではないですかね??
私はこの問題が出題されたのを知って笑ってしまいました。
A.ちなみにこの問題、円に内接する正八角形を求めると証明できます。
※東京大学の入試問題で正八角形、アルキメデスは正96角形、関は正131,1072角形。
江戸数学のレベルの高さが伺えます。
※大学入試や入社面接で結構答えられない質問。
\(円周の長さ=直径×円周率({\pi})\)
円周率 = \(\Large{\frac{円周の長さ}{直径}}\)
円周率とは、円の直径に対する円周の長さの比。
和算の確立
江戸初期、中国から伝わっていたのは三平方の定理や簡単な面積の求め方で、中学数学レベルの内容でした。
関は吉田光由の「塵劫記」から独自に学び、そして江戸時代の数学熱狂でどんどん内容を加速させました。
日本数学レベルを当時の世界の数学と比べても遜色ないレベルにまで仕上げました。
そして日本独自の「和算」というものを確立させたのです。
まとめ
始めは、中学以下レベルでしたが、
- 江戸の数学ブーム
- 関孝和の登場
- 優秀な弟子たち
- 和算の確立
というように世界レベルとなり数学大国となっていました。
江戸時代といえば、歴史で習ったのは飢饉やら改革やら法律やら・・・。たまにはこういう歴史も教えてほしいですね。
ちなみに関は後に「算聖」と呼ばれたと言われています。