
高速道路を作る!
アイルズベリー、ビールズベリー、シールズベリー、ディールズベリーという4つの町があり、これらは1辺1kmの正方形の各頂点にあります。

この4つの町をすべて高速道路で結ぶように仕事の依頼がきた。
費用を抑えるために、最短距離で結びたい。どうすれば最短距離になり、最短距離は何kmだろうか??
解説(間違った考え)
ほとんどの人がやってしまう間違いをまずは解説します。
最短距離ということで、感覚的に直線で結ぶと思ってしまいます。実際に2点ABで考えてみると最短距離は、直線で結んだ距離になります。
なので、この問題の場合は、

このように、2本の対角線を結んでしまいます。
三平方の定理
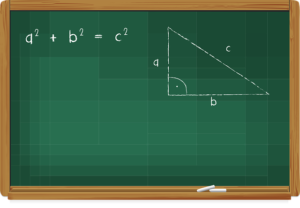
\(1^2+1^2=x^2 \)
\(x=\sqrt{2}\)
\(2×\sqrt{2}=2.82・・\)
となり、約2.82kmとなりますが、これは正解ではありません。
解説(正しい)高校生以上向け
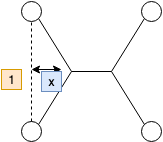
これが答えの形です。
では、最短距離になるにはxがどの値になるのか?
X=0に代入すると、
\(4×\sqrt{0^2+\frac{1}{4}}+1-2×0\)\(4×\frac{1}{2}+1=\Large{3}\)
となります。
x=1/2に代入すると、

先ほどの形となり、\(\Large{2\sqrt{2}}\)となります。
xを0.1、0.2としていけば、近いところにできます。
しかし最短になるのは、ものすごく大変です。
ここで登場するのが、「微分」です!!
ここから読むの根気が要ります。

微分とは、瞬間の変化率を求めることです!
瞬間の変化率とは、つまり「接線の傾き」のことで、この傾きが0の時に、極大か極小値が求まります。
ただ、合成関数の知識などが必要なので、簡単に3点ほど説明。
- x^nの導関数について
- √の指数について
- 合成関数について
x^nの導関数の例題
\(f(x)=3x^2+5x+2\)の関数を微分。
\(f'(x)=2×3x^{2-1}+5×x^{1-1}\)
\(f'(x)=6x+5\)
※x^0=1となります。
合成関数の例題
\(f(x)=(x^2+1)^3\)を微分。
合成関数の公式より
\(f'(x)=3(x^2+1)^2×2x=6x(x^2+1)^2\)
- x^nの導関数について
- √の指数について
- 合成関数について
この知識があれば、
次の解説もわかると思います。
(解説)
\(xの定義域は、0≦x≦\frac{1}{2}\)\(\sqrt{x^2+\frac{1}{4}}=(x^2+\frac{1}{4})^{\frac{1}{2}}\)とあらわす。
(計算)
\(f'(x)=(4×(x^2+\frac{1}{4})^{\frac{1}{2}}+1-2x)'\)
\(=4×\frac{1}{2}×(x^2+\frac{1}{4})^{-\frac{1}{2}}×2x-2\)
\(=4x×(x^2+\frac{1}{4})^{-\frac{1}{2}}-2\)
\(=\frac{4x}{(x^2+\frac{1}{4})^{\frac{1}{2}}}-2\)
これでは今一つわかりずらいので、グラフで確認したいと思います。
そこで、
\(xの定義域は、0≦x≦\frac{1}{2}\)
なので、X=0のときと、X=1/2のときの増減を確認していきます。
こういうグラフが予想されます!
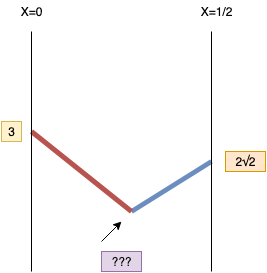
このグラフの???を求めれば、最短距離がわかります。
しかし、どうすればいいのか?
これは、この瞬間の変化が0のとき、求めることができます!
つまりf'(x)=0とすれば、接線の傾きが0になるので、この???がわかります。
ここでXの値がわかったので、???の値は、

\(f(x)=4×\sqrt{x^2+\frac{1}{4}}+1-2x\)
の式に\(x=\frac{1}{2\sqrt{3}}\)を代入すれば求めれます。
よって、2.73kmとなります!
シュタイナー木問題
この問題は、シュタイナー木問題と呼ばれています。特にこの正方形の形は有名です。
日本数学オリンピックの予選にも出題されました。(1993)
最後に平面上3点のシュタイナー木問題を簡単に紹介します。

このことを知っていたとして、先ほどの問題を考えていきます。

まずは、この形にします。
そして、交わる点をPとして、⊿ABPと⊿CDPで考えてみます。

2つの三角形はどの内角も120°を超えていないため、最短距離は三角形の内側になり、その角度は120°となる点になります。
よって、この形となります。

最短距離については、直角三角形の30°,60°,90°の1:2:√3の法則を知っていれば簡単です。
\(1:\sqrt{3}=x:\frac{1}{2}\)
\(\sqrt{3}x=\frac{1}{2}\)
\(x=\frac{1}{2\sqrt{3}}\)
このようにして、解くことも可能です。





















